はじめに
この記事はこちらの記事の続きとなっております。
前回の記事を見ていない方は先にそちらから見てください。
また、今回ブログで解説する内容はこちらのスライドに含まれています。
スライドの方がわかりやすいと言う方はそちらをご覧ください。
この記事では前回に引き続き、Ear Clipping Algorithmについて解説します。
前回は三角形分割に一つ条件式をいれることで、
複雑な多角形を三角形に分割できたと言ったところでした。
しかし前回の処理ではまだ対応できない多角形がある状態となっています。
現状の問題
1. 図のような多角形ABCDEFGHについて考えます

2. 前回、前々回と同じ流れで三角形をキャッシュしていきます




なんだか雲行きが怪しい...。

もうダメそうですが、最後までやり切りましょう。


というわけで、このような多角形ではまた三角形の分割が失敗してしまいます。
今回もこんな多角形を綺麗に分割できる方法を紹介します。
解決方法
三角形をキャッシュするときにさらに条件をつける
Ear Clipping Algorithmについて書かれている論文にはこんなことも書いてありました。
連続する3つの頂点 V0、V1、および V2によって形成される三角形で、頂点V1が凸頂点であるものが条件。
凸頂点とは、その頂点での内角がπラジアン未満である。
An ear of a polygon is a triangle formed by three consecutive vertices Vi0 , Vi1 , and Vi2 for which Vi1 is a convex vertex. At such a vertex, the interior angle at the vertex is smaller than π radians.
つまりどういうことか?
三角形ができた時、頂点の内角が180°を超えているかどうかを確認する必要があります。
(πラジアン = 180°)
この場合内角とは「頂点から見て多角形側の角度」を指します。
三角形の中の角度とは限らないので注意が必要です。
先程の手順を交えて説明します。
三角形ABHの場合

画像の水色の部分が外角になり、青色の角度が内角になります。
この場合、内角は180°より小さいので問題ありません。
三角形DEHの場合

この場合、内角は三角形側ではなく多角形側(三角形の外)に作られます。
画像の青い角度のことですね。
この角度は180°より大きいため、問題ありと判断します。
そのため、この三角形DEHはキャッシュせず、処理をスキップします。
内角が180°を超えているかの確認方法
難しそうに見えますが、実はこれは簡単に求められます。
これはその三角形が右回りか左回りかを調べるだけです。
右回りだったら内角が180°を超えるのが確定します。

▶︎補足(折りたたみ)
今回は多角形の頂点を左回りに並べているため、三角形が右回りだったら180°を超えていると判定ができています。
逆に多角形の頂点が右回りに並んでいた場合は、三角形が左回りだったら180°を超えていると判定ができます。
多角形の頂点が左回りか右回りかで判定が逆になるので気をつけてください。
条件の更新

この条件を今までの条件に加えた手順はこちらになります。
- 多角形の頂点を左回り(反時計回り)にして用意
- 頂点を1つ1つチェックし、左右の頂点と合わせて三角形を作る
- その三角形の中に残りの頂点が含まれていないかをチェックする
- 三角形の中に残りの頂点が含まれていた場合、キャッシュせず次の頂点についてチェックする(2に戻る)
- 3~4で問題なかった場合はさらにその三角形が左回りか右回りかチェックする
- 右回りだった場合、キャッシュも頂点の削除もせず、次の頂点についてチェックする(2に戻る)
- 2~6を繰り返す
- 頂点の残りが3つになったらその3つで三角形を作ってキャッシュする
- キャッシュされた三角形を全て描画すると多角形ができる
だいぶ複雑な処理になってきました。
手法の流れの解説
では、前回と同じく再度同じ多角形に対して、
新たに条件を加えた状態で処理していきましょう。
1. 再度多角形ABCDEFGHについて考える

2. 三角形ABHについて考える

キャッシュして頂点Aを削除します。
3. 三角形BCHについて考える

キャッシュして頂点Bを削除します。
4. 三角形CDHについて考える

三角形CDHをキッシュして頂点Cを削除します。
5. 三角形DEHについて考える
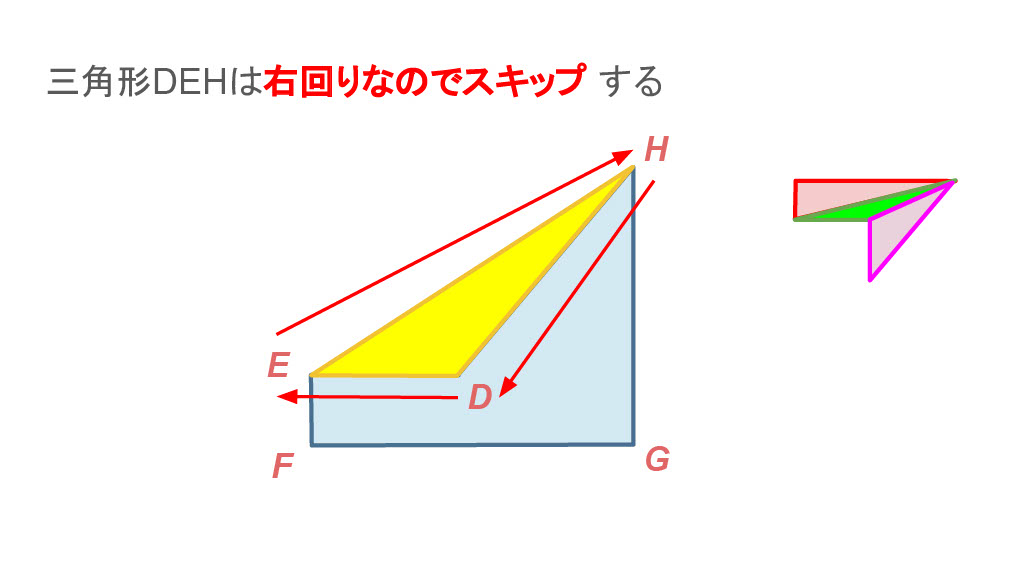
この場合は三角形DEHをキャッシュせず、頂点Dも消しません。
6. 頂点Dをスキップして、頂点Eについて考える

すると、三角形EFDは左回りですね。
中に頂点も含んでいないので問題ありません。
キャッシュして頂点Eを削除します。
7. 頭に戻って頂点Dについて考える

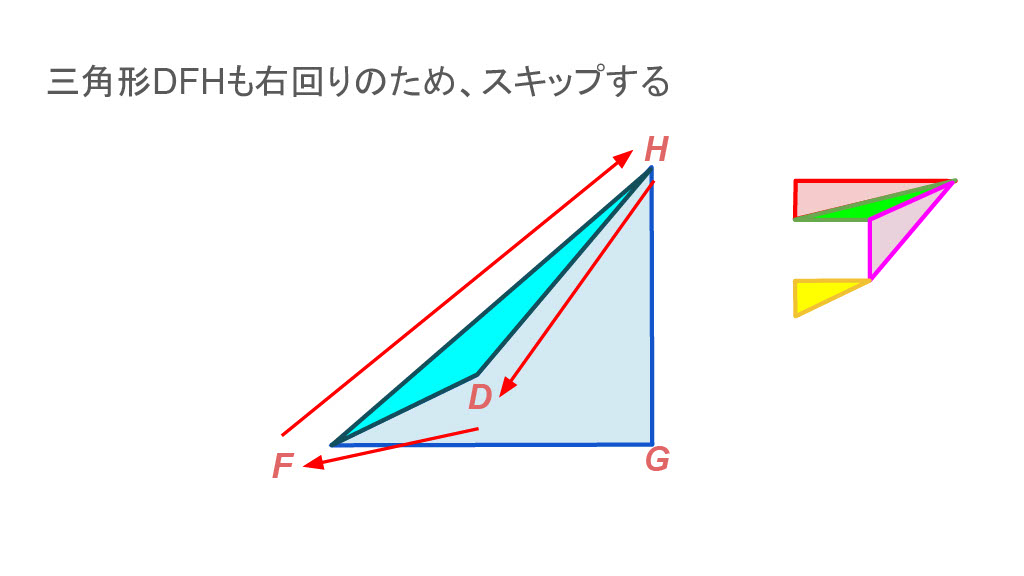
キャッシュせず頂点も消しません。スキップします。
8. 次の頂点Fについて考える

こちらは左回りですので問題ありません。
三角形FGDをキャッシュして頂点Fを削除します。
9. 頂点Fを削除して、残りの多角形を考える

10. 完成

これが真のEar Clipping Algorithmです。
GMLで実装
では前回、前々回の記事と同じく、先ほどの判定をGMLで記述しましょう。
三角形が左回りか右回りかを求める方法
例えば、三角形ABCが左回りか右回りかを求めたい場合は
- ABベクトルとACベクトルを求める
- その2つのベクトルの外積がプラスなら左回りと判断できる
という感じです。
かなりシンプルですが、注意が必要なのは三角形の頂点の順番です。
これが三角形BACだとしたら結果が全然別のものになります。
三角形の順番は必ずルール通りに並べてください。
GMLで関数を用意
先程の処理をGMLで書いてみましょう。
/** * 三つの頂点の外積が正であるかを判定します。 * @param {Vector2} _prev - 前の頂点。 * @param {Vector2} _current - 現在の頂点。 * @param {Vector2} _next - 次の頂点。 * @returns {bool} 外積が正であればtrue。 */ function is_positive_cross_product(_prev, _current, _next) { var _dx1 = _current.x - _prev.x; var _dy1 = _current.y - _prev.y; var _dx2 = _next.x - _current.x; var _dy2 = _next.y - _current.y; var _cross = _dx1 * _dy2 - _dy1 * _dx2; return _cross > 0; }
これだけです。簡単ですね!!
三角形分割のロジックに組み込み
最後は、先程のチェック処理を分割処理に組み込みましょう。
前回作ったis_ear_vertex関数にチェック処理を追加します。
/** * 頂点が耳かどうかを判定する * @param {Vector2} _prev - 前の頂点 * @param {Vector2} _current - 現在の頂点 * @param {Vector2} _next - 次の頂点 * @param {array<Vector2>} _polygon - ポリゴンの頂点配列 * @returns {bool} 耳であればtrue */ function is_ear_vertex(_prev, _current, _next, _polygon){ // 三角形が左回りか右回りかを判定する // 外積が正の場合、3つの頂点 (_prev, _current, _next) は右回り(時計回り)) // Ear Clipping Algorithmでは左回りが有効な三角形の条件なので、右回りの場合は無効として false を返す if (is_positive_cross_product(_prev, _current, _next)) { return false; } // ポリゴン内のすべての頂点をチェック for (var _i = 0; _i < array_length(_polygon); _i++) { var _point = _polygon[_i]; // 現在チェック中の頂点 // 今チェックしている頂点と同じだったら処理をスキップするための条件式 var _isSamePoint = !_point.VectorEquals(_prev) && !_point.VectorEquals(_current) && !_point.VectorEquals(_next); // 今チェックしている頂点と同じじゃなくて // 尚且つ現在の点が三角形の内部にある場合、三角形は不正とみなす if (_isSamePoint && point_in_triangle(_point.x, _point.y, _prev.x, _prev.y, _current.x, _current.y, _next.x, _next.y)) { return false; } } // 問題がなければ三角形は有効と判定 return true; }
既にメインのループ処理にこちらの関数は組み込まれているので、
変更する箇所はここだけになります。
結果
では、先ほどのコードを組み込んだ処理を試してみましょう。
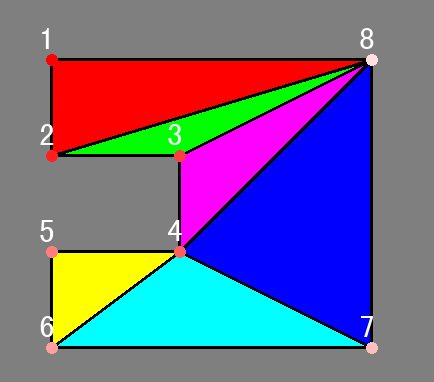
これで完璧です!
まとめ
今回は耳かどうかの判定処理をさらに強化しました。
これらの条件を加えることで、多角形を綺麗に三角形に分割をすることが可能になります。
綺麗に三角形分割ができたところで、
次回はついに、スプライトを描画していこうと思います。
